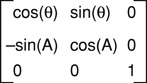先日、携帯で QuickTime の .mov 動画を撮ったら、90°傾いて撮れてしまいました。iPhone 3GS のカメラでは、ときどき向きがおかしくなります。.mov を .mov のまま90°回転する無料のソフトを探したものの見つからず、直接バイナリエディタで向きを書き換えてみました。
以下、自分用のメモです。たまたまうまくいったように思えるだけで、実はファイルがめちゃくちゃに壊れているかもしれませんのであしからず。
要約
- iPhone 3GS で撮影した QuickTime の .mov ムービーを前提とする。
- 元の .mov ファイルは保存して、コピーした .mov ファイルをバイナリエディタで開いて編集。
- 文字列 ‘moov’ を検索。その下の文字列 ‘mvhd’ を探す。ファイルの下の方にあるはず。
- Figure 2-3 The layout of a movie header atom | QuickTime File Format Specification: Movie Atoms を参考に、アフィン変換の行列、Matrix structure (a, b, u, c, d, v, x, y, w) を見つける。w の 40 00 00 00（16進） の並びが目安。
- The Transformation Matrix | QuickTime Movie Creation Guide: Creating Movies の回転行列の式を参考に、(a b c d) を書き換える。x軸は右向き、y軸は下向き、角度は時計回りが正。固定小数点 16.16 形式なので、1 なら 00 01 00 00、-1 なら ff ff 00 00 。90度ごとの回転なら、値は 0 か 1 か -1 の組み合わせとなる。よく見かける回転行列の転置行列になっている。
- 再生してみて、希望通りに回転していれば O.K. のはず。
- （ファイルによっては、ほかの ‘mvhd’ のところの (a b c d) を書き換える必要があるかもしれない）
詳細と雑談
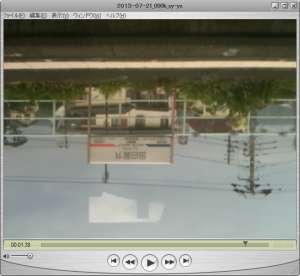
ランドスケープ（横長）のつもりで撮影したのに、ポートレイト（縦長）で記録された映像：
このファイルをバイナリエディタで開きます。直接書き換えるので、オリジナルのファイルは保存、コピーした作業用のファイルに対して操作します。無理やり操作するので、たいてい何回も間違えます。さて、QuickTime ムービー (.mov) ファイルの構造を仕様書で調べます。
まず、書き換えるべき値 Matrix structure の目印の文字列を探します。
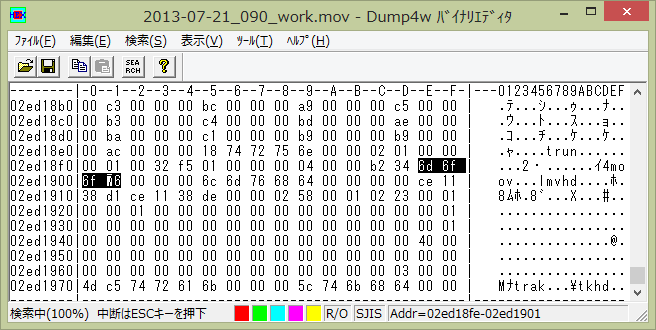
より、バイナリエディタで Movie atom の文字列 ‘moov’ を検索し、すぐ下の Movie header atom の文字列 ‘mvhd’ を探します。（今回扱っている動画ファイルの場合、ヘッダと言いつつ、頭のほうではなくファイルの一番下の方にあります。’mvhd’ だけで検索すると、上の方にもありますが、こちらを書き換えても動画の向きは変わりませんでした。）
文字列 ‘mvhd’ がある Movie header atom の構造は、
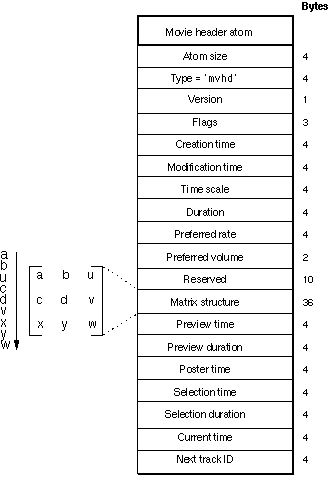（図：同上より）
この Matrix structure のうち、[a b c d] を使って回転します。文字列 ‘mvhd’ があるのが Movie header atom の5～8バイトめ。次の Version から Reserved まで 1 + 3 + 4 + 4 + 4 + 4 + 4 + 2 + 10 ( = 36 )バイトあるので、Matrix structure の要素 a の先頭は ‘mvhd’ の ‘d’ の次から 37 バイト目です。こんな感じにがんばって数えていくと、この .mov ファイルの場合は
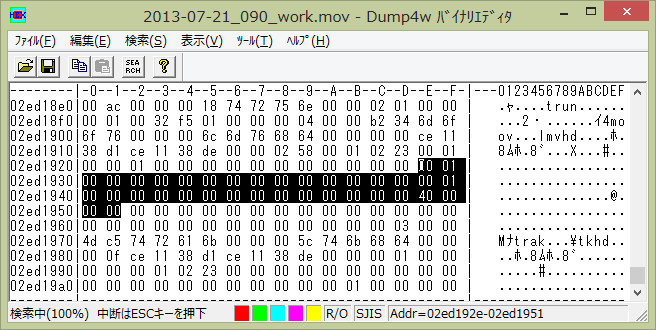
a = &h 00 01 00 00 = 1.0
b = &h 00 00 00 00 = 0.0
u = &h 00 00 00 00 = 0.0
c = &h 00 00 00 00 = 0.0
d = &h 00 01 00 00 = 1.0
v = &h 00 00 00 00 = 0.0
x = &h 00 00 00 00 = 0.0
y = &h 00 00 00 00 = 0.0
w = &h 40 00 00 00 = 1.0
$$ \left( \begin{array}{ccc} a & b & u \\ c & d & v \\ t_x & t_y & w \end{array}\right) = \left( \begin{array}{ccc} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 1.0 \end{array}\right) $$
となっています。各 4 バイトは固定小数点で、a, b, c, d, x, y は 16.16 ビット、u, v, w は 2.30 ビットの区切りです。行列と数値の形式は次の通り：
（図：同上より）
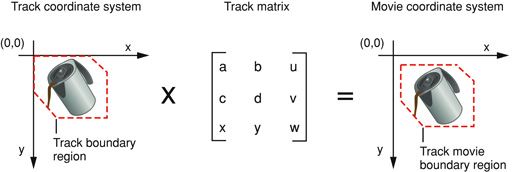
アフィン変換というもので、一次変換と平行移動を同時に表現しているそうです。
QuickTime では、高校数学の回転行列や一次変換で見慣れた行列の形式と違って、その転置行列で表現しているようです。
このへんのことは、別の文書にもう少し詳しく書いてありました。
によると、平面の x 軸、y 軸の向きは
（図：同上より）
となっているようで、y 軸が上でなく下に向いています。
によると、常に u = v ≡ 0.0 、w ≡ 1.0 と書いてあります。つまり w は常に &h 40 00 00 00 となります。変換行列の末尾に必ず 40 が現れるので、これが探す目安になります。
回転行列のところでは、
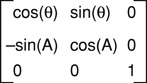（図：同上より）
角度が q、θ、A と混乱していますが、同じ文字の誤植でしょう。また、回転の向きが反時計回り counterclockwise に角度 q と書いてありますが、その逆で、画面を見る人から見れば時計回りと考えられます。一般的な平面座標では x 軸が右向きで y 軸が上向きであり、x 軸から y 軸に向かう方向となる反時計回りが角度の正の向きです。しかし、QuickTime のように y 軸が下向きならば、x 軸から y 軸に向かう方向となる時計回りが正と考えるのが自然です。式の形からも、そうでないとおかしいでしょう。
さて、画像の中心が原点なら平行移動は不要なので、回転は (a b c d) の組だけ考えればいいはずです（原点は左上ではないかと思うのですが、勝手にセンタリングしてくれるようです）。
問題の映像ファイルの回転に関わる数値だけ行列で抜き出すと、
$$ \left( \begin{array}{cc} a & b \\ c & d\end{array}\right) = \left( \begin{array}{cc} 1.0 & 0.0 \\ 0.0 & 1.0\end{array}\right) $$
$$ \left( \begin{array}{cc} x^\prime & y^\prime \end{array} \right) = \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} a & b \\ c & d\end{array}\right) = \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} 1.0 & 0.0 \\ 0.0 & 1.0\end{array}\right) = \left( \begin{array}{cc} x & y \end{array} \right) $$
つまり、単位行列です。90°回転されているようにみえるこの映像は、内部的に QuickTime のファイルとしては回転されていませんし、ほかの変換（マッピング）もされていません。
試しに、x と y を入れ替えるような行列にすると、
$$
\left( \begin{array}{cc} x^\prime & y^\prime \end{array} \right)
= \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} a & b \\ c & d\end{array}\right)
= \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} 0.0 & 1.0 \\ 1.0 & 0.0\end{array}\right)
= \left( \begin{array}{cc} y & x \end{array} \right) $$
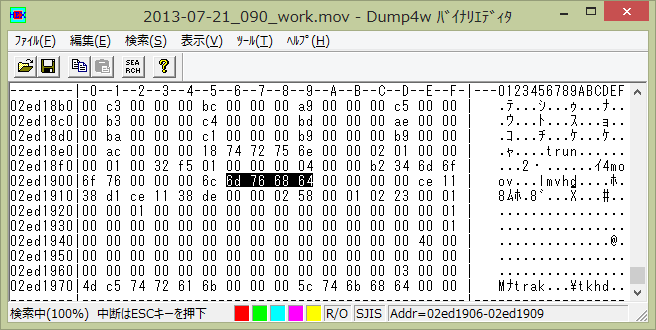
w の &h40 を目安に、その上の方の &h01 の2カ所をバイナリエディタで探して、それぞれ別の場所に書き換えます。
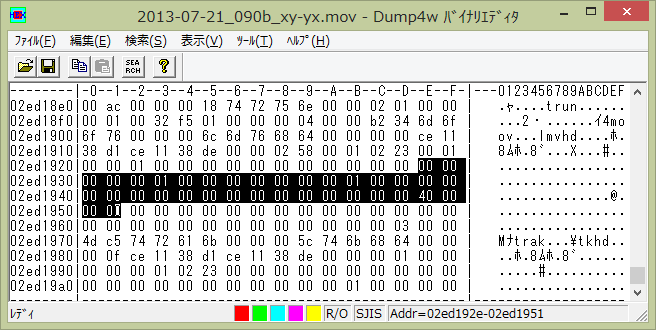
90°の傾きは解消しましたが、天地が反転した映像になりました。駅名の文字も裏返っています。この動画を、さらに y’ を反転させればよさそうです。
$$
\left( \begin{array}{cc} x^\prime & y^\prime \end{array} \right)
= \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} a & b \\ c & d\end{array}\right)
= \left( \begin{array}{cc} x & y \end{array} \right) \left( \begin{array}{cc} 0.0 & -1.0 \\ 1.0 & 0.0\end{array}\right)
= \left( \begin{array}{cc} y & -x \end{array} \right) $$
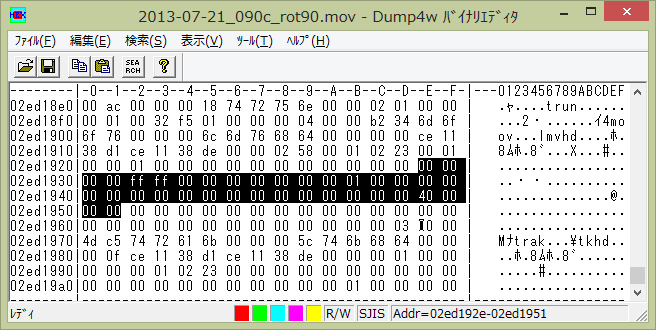
-1.0 は整数部を2の補数にして &h ff ff 00 00
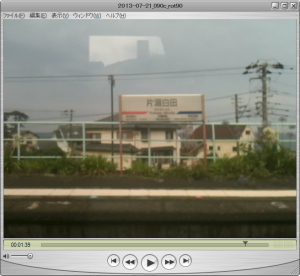
映像の最後のほうで駅のホームの文字が読めるので、裏返しにはなっていません。空と海の位置関係から上下も合っています。正常に反時計回りに 90° 回転できたように思われます。’mvhd’ で検索するともう一ヵ所あるので、そちらも直すべきなのかもしれませんが、今回は放置しました。ともかく、これで書き換えは成功したということにします。
さて、よく見かける回転行列は、角度をθとして
$$
\left( \begin{array}{c} x^\prime \\ y^\prime \end{array}\right)
=\left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)
\left( \begin{array}{c} x \\ y \end{array}\right) $$
ですが、QuickTime では転置した形で書いてあるので
$$
\left( \begin{array}{cc} x^\prime & y^\prime \end{array}\right)
=\left( \begin{array}{cc} x & y \end{array}\right)
\left( \begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right) $$
です。Matrix structure（アフィン変換）全体も同じく転置行列になっています。
反時計回りに 90° 回転するとき、上述のように時計回りが正なので θ ＝ －90° 、QuickTime の方の式で
$$
\left( \begin{array}{cc} x^\prime & y^\prime \end{array}\right)
=\left( \begin{array}{cc} x & y \end{array}\right)
\left( \begin{array}{cc} \cos (-90) & \sin (-90) \\ -\sin (-90) & \cos (-90)\end{array}\right)
=\left( \begin{array}{cc} x & y \end{array}\right)
\left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right)
=\left( \begin{array}{cc} y & -x \end{array}\right) $$
試行錯誤的に成功したときの行列と一致します。回転方向が普通と逆で時計回りが正だということに気がつくまでずいぶんかかりました。試行錯誤で回転はできたものの、Apple の解説に書いてあることと一致しないので、どこを間違えたのだろうかと悩みました。（もちろん、今でも私が間違っている可能性があります）
ところで、映像の回転については、はじめは iPhone の splice というアプリを試しました。
しかし、この動画についてはうまく読み込めないようです。いろいろ検索語をかえながら探していたら、PC の QuickTime Pro なら回転の編集が一瞬で終わるとのこと。一瞬ということなら、ヘッダを書き換えるだけでよいはず。それでみつけて参考にしたのが、
Apple のデベロッパーセンターからダウンロードできる dumpster というツールを使うのですが、運が悪いことに、
の直後であちこちダウンしたまま、登録できず、なにもダウンロードできずという状態でした。ほかのサイトからダウンロードできるのは dumpster の Win32 ビット版のみで、そのサイトによると、もともと 64 ビット版はないらしい。QuickTime atom をいじるほかのツールも Apple デベロッパー センターがダウンしていてダウンロードできず。
で概要を読むと、自分でプログラムを作って利用できなくはないようでした。さらに検索していたら
などがでてきて、バイナリエディタだけでもちょっとした書き換えならどうにかなりそう。ということでやってみました。
正規の QuickTime のライブラリをきちんと使っているソフトなら変換行列を使うのでしょうが、向きを決め打ちで表示しているソフトでは90°傾いたままなのでしょうね。それ以前に、ひょっとして、この書き換えで不整合を生じて、読み込みさえ不能の可能性もあり？ いやいや、この程度の書き換えなら大丈夫ですよね。仕様書や解説は matrix のところを拾い読みしただけなので、一抹の不安が残っています。
(2013/7/31)
(2013/8/8) サムネイル画像追加
(2025/2/8) 数式描画を MathJax に変更
